今天一共写了两道电路大题,一题是九大综合理工的,主要考点是网孔电流法。
另一题是东工电气的一道考题,考点是戴维南和叠加定理,私以为这题非常巧妙,甚至可以成为叠加定理理解的最后重要环节,于是将其放上博客;但是因为篇幅较长,可能一时半会比较难完工。
首先附上这道题:

1)是比较简单的戴维南等效电路。
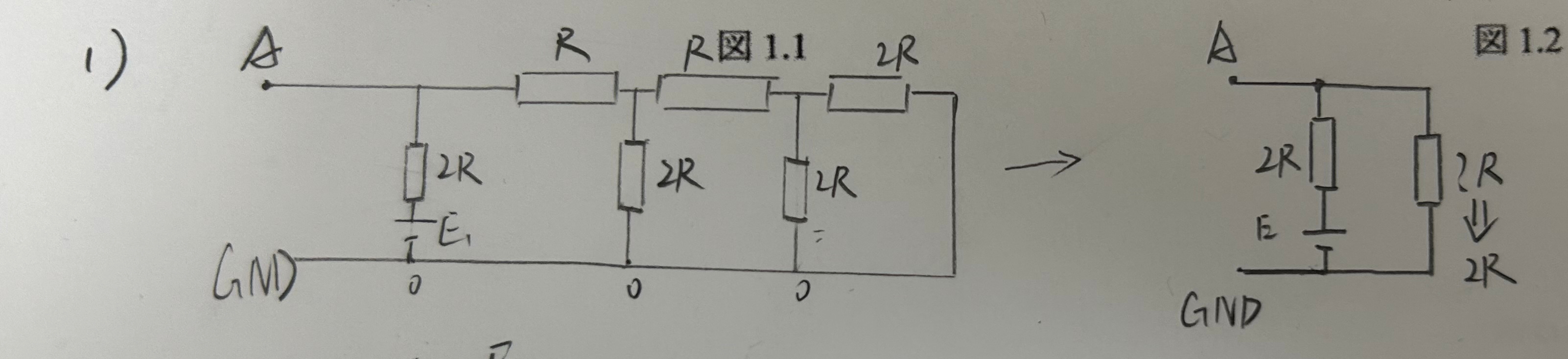
计算得出:
$$
V_A = \frac{E1}{2}
$$
2)依旧是等效电路,稍微加点计算过程吧
计算过程:
$$
R_o = \frac{1}{\frac{1}{3R} + \frac{1}{2R}} = \frac{6}{5} R
$$
$$
V_o = \frac{\frac{6}{5} R}{\frac{6}{5} R + 2R} \cdot E = \frac{3}{8} E
$$
$$
V_A = \frac{3}{8} E \cdot \frac{2R}{2R + R} = \frac{1}{4} E_2
$$
3)第三问烦一点,嗯算就完事了
计算得出:
$$
V_A = \frac{E3}{8}
$$
4)第四问,对他使用叠加定理吧
$$
V_A = \frac{E1}{2} +\frac{1}{4} E_2+\frac{E3}{8}
$$
5)很好算,第一问都把它等效的差不多了
$$
R_{\text{等效}} = \frac{1}{\frac{1}{2R} + \frac{1}{2R}} = R
$$
6)其实就是4和5的答案,等效电路
$$
R_o =R
$$
$$
E_o = \frac{E1}{2} +\frac{1}{4} E_2+\frac{E3}{8}
$$
7)先画一个图
$$
V_A = \frac{R_L}{R_o + R_L} \cdot E_0
$$
$$
= \frac{R_L}{R_o + R_L} \cdot \left(\frac{E_1}{2} + \frac{E_2}{4} + \frac{E_3}{8} \right)
$$
